IT's 2 EG
세그먼트 트리(Segment Tree) 본문
세그먼트 트리란?
세그먼트 트리는 각 노드에 특정 구간의 대표값을 저장함으로써, 특정 구간에 대한 질문을 빠르게 답하는데 사용합니다. 세그먼트 트리는 완전 이진트리의 형태를 가지며 각 노드의 자식 노드는 부모 노드의 구간을 이등분한 두 개의 구간 중 한쪽 구간에 대한 정보를 가지게 됩니다.
이를 통해 세그먼트 트리를 활용한 연산은 최고 O(logN)의 시간복잡도를 가지게 됩니다.
세그먼트 트리 생성 방법
세그먼트 트리를 활용한 대표적인 문제는 특정 구간의 합을 구하는 것입니다.
아래는 0부터 9까지 N이 10인 배열에 대한 구간합을 세그먼트 트리로 구성하는 방법입니다.
1번 최상단 노드는 0부터 9까지의 구간합을 반환하도록 설정합니다.
자식노드인 2번과 3번 노드에는 1번 노드의 범위에 절반씩 분할하여 구간합을 반환하도록 설정합니다.
즉, 2번 노드는 0에서 4까지의 대표값을 3번 노드는 5에서 9까지의 구간합을 저장합니다.
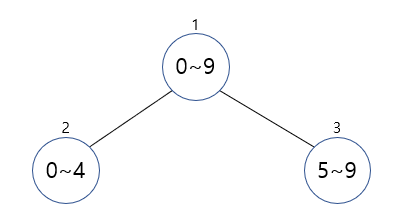
이는 재귀함수를 통해서 쉽게 구현이 가능합니다.
부모 노드의 번호가 n이라면 왼쪽 자식노드의 번호는 n*2, 오른쪽 자식 노드의 번호는 n*2+1 입니다.
보무 노드의 담당구간이 [start, end]이고, 중간값인 mid = (start + end) / 2 입니다.
이때 왼쪽 자식노드는 [start, mid] 오른쪽 자식 노드는 [mid, end] 입니다.
위와 같은 연산을 sp 와 ep가 같은 리프노드까지 반복하여 생성을 합니다.
이를 소스코드로 표현하면 아래와 같습니다.
//arr: 주어진 배열
//tree: arr의 세그먼트 트리
//start: 시작 노드, end: 끝 노드
int init(vector<int> &arr, vector<int> &tree, int node, int start, int end)
{
if (start == end) return tree[node] = arr[start]; //리프노드에 대한 연산
int mid = (start + end) / 2; //중간 노드 연산
//부모노드와 자식노드간의 연산
return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
}
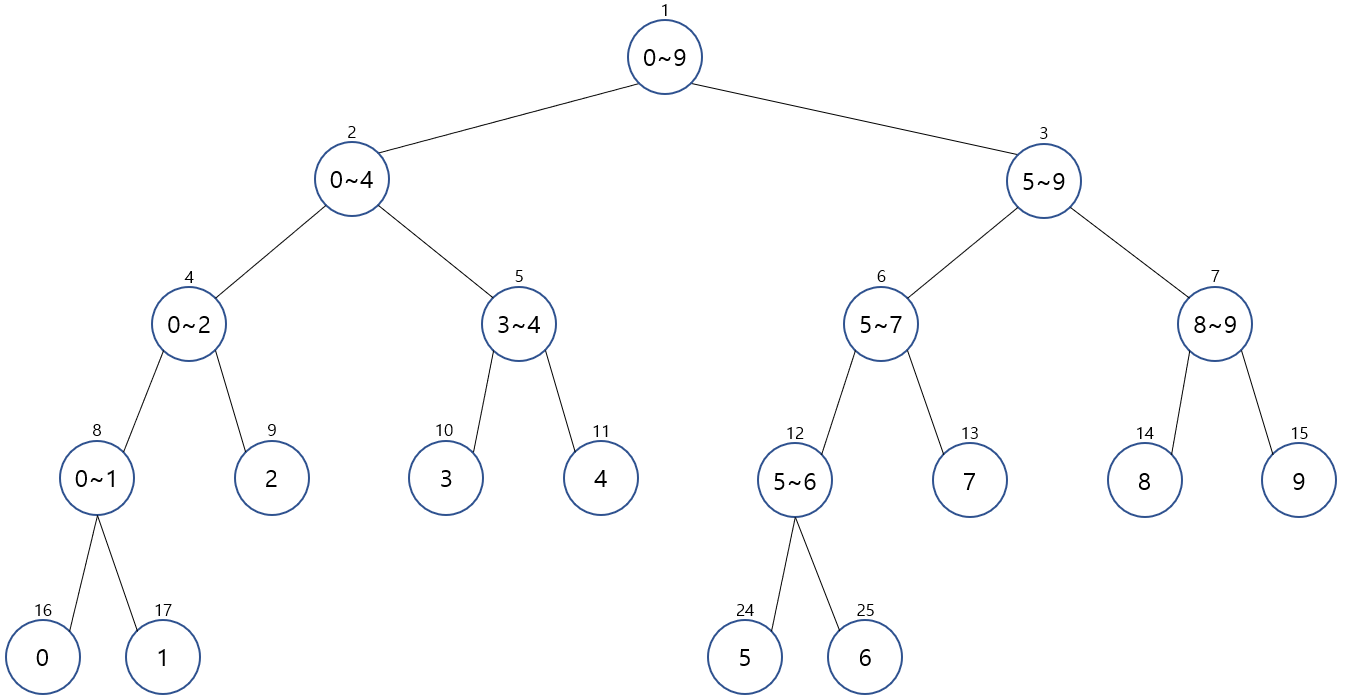
최종적으로 생성된 세그먼트 트리의 형태는 아래와 같습니다.
참고로 세그먼트 트리의 높이는 H = [lgN]이고, 총 노드의 개수는 2^(H+1)개 입니다.
세그먼트 트리 탐색 방법
노드가 담당하고 있는 구간을 A = [start, end]이고, 구해야하는 구간이 B = [left, right]일때 아래의 4가지 경우가 존재합니다.
1. A와 B가 겹치지 않는경우 : left > end || right < start
2. B가 A를 포함하는 경우 : left <= start && right >= end
3. A가 B를 포함하는 경우 : left >= start && right <= end
4. 일부 겹치는 경우 : 1,2,3을 제외한 나머지
1번의 경우 겹치는 구간이 존재하지 않기 때문에 더이상 탐색을 할 필요가 없이 0을 리턴합니다.
2번의 경우 구해야 하는 구간이 현재 노드의 구간을 포함하기에 추가 탐색 없이 tree[node]값을 리턴합니다.
3,4번의 경우 구해야 하는 구간이 현재 노드의 일부이기에 추가 탐색을 진행합니다.
int sum(vector<int> &tree, int node, int start, int end, int left, int right)
{
// [left, right]가 [start, end]와 겹치지 않는 경우
if (left > end || right < start) return 0;
// [left, right]가 [start, end]를 완전히 포함하는 경우
if (left <= start && end <= right) return tree[node];
// [start, end]가 [left, right]를 완전히 포함하는 경우 or [left, right]와 [start, end]가 겹쳐져 있는 경우
return sum(tree, node * 2, start, (start + end) / 2, left, right) + sum(tree, node * 2 + 1, (start + end) / 2 + 1, end, left, right);
}세그먼트 트리 알고리즘 예제
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
#include <iostream>
#include <cstdio>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
int N, M, K; //N: 수의 개수, M: 수의 변경이 일어나는 회수, K: 구간의 합을 구하는 회수
//세그먼트 트리 구성
long long init(vector<long long> &a, vector<long long> &tree, int node, int start, int end)
{
if (start == end)
{
return tree[node] = a[start];
}
else
{
return tree[node] = init(a, tree, node * 2, start, (start + end) / 2) + init(a, tree, node * 2 + 1, (start + end) / 2 + 1, end);
}
}
//중간의 어떤 수를 변경
void update(vector<long long> &tree, int node, int start, int end, int index, long long diff)
{
//index가 [start, end]내에 없으면 종료
if (index < start || index > end) return;
//범위내에 있으면 해당 노드의 값에 diff(차이값)을 더한다
tree[node] = tree[node] + diff;
//하위 노드에서 추가적인 값을 구하기 위해 더해준다.
if (start != end)
{
update(tree, node * 2, start, (start + end) / 2, index, diff);
update(tree, node * 2 + 1, (start + end) / 2 + 1, end, index, diff);
}
}
//구간의 합을 구하기 위한 함수 (left ~ right)
long long sum(vector<long long> &tree, int node, int start, int end, int left, int right)
{
// [left, right]가 [start, end]와 겹치지 않는 경우
if (left > end || right < start) return 0;
// [left, right]가 [start, end]를 완전히 포함하는 경우
if (left <= start && end <= right) return tree[node];
// [start, end]가 [left, right]를 완전히 포함하는 경우 or [left, right]와 [start, end]가 겹쳐져 있는 경우
return sum(tree, node * 2, start, (start + end) / 2, left, right) + sum(tree, node * 2 + 1, (start + end) / 2 + 1, end, left, right);
}
int main(int argc, char* argv[])
{
int N, M, K; //N: 수의 개수, M: 수의 변경이 일어나는 회수, K: 구간의 합을 구하는 회수
scanf("%d %d %d", &N, &M, &K);
vector<long long> a(N);
int h = (int)ceil(log2(N)); //세그먼트 트리의 높이를 의미, ceil(): 소수점 이하 모두 올림
int tree_size = (1 << (h + 1)); //트리의 크기, 2^(h+1) - 1
vector<long long> tree(tree_size);
M += K;
for (int i = 0; i < N; i++)
scanf("%lld", &a[i]);
init(a, tree, 1, 0, N - 1);
while (M--)
{
int t1;
scanf("%d", &t1);
if (t1 == 1)
{
int t2;
long long t3;
scanf("%d %lld", &t2, &t3);
t2 -= 1;
long long diff = t3 - a[t2];
a[t2] = t3;
update(tree, 1, 0, N - 1, t2, diff);
}
else if (t1 == 2)
{
int t2, t3;
scanf("%d %d", &t2, &t3);
printf("%lld\n", sum(tree, 1, 0, N - 1, t2 - 1, t3 - 1));
}
}
return 0;
}'알고리즘 > 이론' 카테고리의 다른 글
| 유클리드 호제법(Euclidean Algorithm) (0) | 2017.06.25 |
|---|---|
| 유니온 파인드(Union-Find, Disjoint Set) (0) | 2017.06.16 |
| 플로이드-워셜(Floyd-Warshall) (0) | 2017.06.11 |
| 다익스트라(Dijkstra) (0) | 2017.06.11 |
| 이진탐색(Binary Search) (0) | 2017.05.22 |



