IT's 2 EG
플로이드-워셜(Floyd-Warshall) 본문
플로이드-워셜 알고리즘 이란?
플로이드-워셜 알고리즘은 다이나믹 프로그래밍 접근 방식으로 그래프 상의 모든 두 정점에 대한 경로의 최단거리를 구합니다. 다익스트라 알고리즘과 달리 음수 가중치를 가지는 경로가 포함되어 있어도 최단거리를 구할 수 있습니다. 시간 복잡도는 O(V^3)을 가지며, 특정 경로 안에 무수히 많은 경로가 있을때, 중간 정점들이 각각 최단이 된다면 이를 모두 이은 경로 또한 최단이 된다는 개념을 사용합니다.
플로이드-워셜 계산 과정
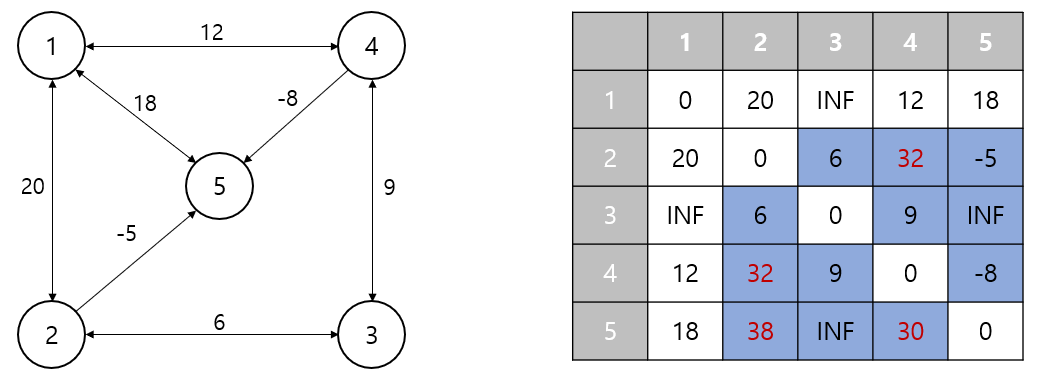
다음은 예제 그래프를 통해 플로이드-워셜 알고리즘을 통해 서로 다른 두 정점의 최단거리를 구하는 방식입니다.
최초 예제 그래프의 인접한 두 정점간의 거리를 아래와 같이 이차원 배열 형태로 정의합니다.
이후, 각 정점을 중간노드로 경유해가는 과정에서 최소값을 갱신합니다.

우선 1번 정점을 중간노드로 경유할 때 최단거리의 변화입니다.
2번 → 1번 →4번 이동거리가 32로 기존 최단거리보다 작으므로 값을 갱신합니다.
4번 → 1번 →2번 이동거리가 32로 기존 최단거리보다 작으므로 값을 갱신합니다.
5번 → 1번 →2번 이동거리가 38로 기존 최단거리보다 작으므로 값을 갱신합니다.
5번 → 1번 →4번 이동거리가 30으로 기존 최단거리보다 작으므로 값을 갱신합니다.
다음은 2번 정점을 중간노드로 경유할 때 최단거리의 변화입니다.
1번 → 2번 → 3번 이동거리가 26으로 기존 최단거리보다 작으므로 값을 갱신합니다.
1번 → 2번 → 5번 이동거리가 15로 기존 최단거리보다 작으므로 값을 갱신합니다.
3번 → 2번 → 1번 이동거리가 26으로 기존 최단거리보다 작으므로 값을 갱신합니다.
3번 → 2번 → 5번 이동거리가 1로 기존 최단거리보다 작으므로 값을 갱신합니다.
5번 → 2번 → 3번 이동거리가 44로 기존 최단거리보다 작으므로 값을 갱신합니다.

다음은 3번 정점을 중간노드로 경유할 때 최단거리의 변화입니다.
2번 → 3번 → 4번 이동거리가 15로 기존 최단거리보다 작으므로 값을 갱신합니다.
4번 → 3번 → 2번 이동거리가 15로 기존 최단거리보다 작으므로 값을 갱신합니다.

다음은 4번 정점을 중간노드로 경유할 때 최단거리의 변화입니다.
1번 → 4번 → 3번 이동거리가 21로 기존 최단거리보다 작으므로 값을 갱신합니다.
1번 → 4번 → 5번 이동거리가 4로 기존 최단거리보다 작으므로 값을 갱신합니다.
3번 → 4번 → 1번 이동거리가 21로 기존 최단거리보다 작으므로 값을 갱신합니다.

마지막으로 5번 정점을 중간노드로 경유할 때 최단거리의 변화입니다.
2번 → 5번 → 1번 이동거리가 13으로 기존 최단거리보다 작으므로 값을 갱신합니다.
3번 → 5번 → 1번 이동거리가 19로 기존 최단거리보다 작으므로 값을 갱신합니다.
4번 → 5번 → 1번 이동거리가 10으로 기존 최단거리보다 작으므로 값을 갱신합니다.

마지막 점정까지 중간노드 경유를 마치고 최종 행렬이 두 정점사이의 최단거리를 의미합니다.
플로이드-워셜 알고리즘 예제
11403번: 경로 찾기
가중치 없는 방향 그래프 G가 주어졌을 때, 모든 정점 (i, j)에 대해서, i에서 j로 가는 경로가 있는지 없는지 구하는 프로그램을 작성하시오.
www.acmicpc.net
#include <iostream>
#include <cstdio>
#define INF 1000
using namespace std;
int N; // graph size
int graph[101][101];
int DP[101][101];
int main()
{
scanf("%d", &N);
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
scanf("%d", &graph[i][j]);
if (graph[i][j] == 0)
DP[i][j] = INF;
else
DP[i][j] = graph[i][j];
}
}
//플로이드-워셜 알고리즘
for (int k = 1; k <= N; k++)
{
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
if (DP[i][j] > DP[i][k] + DP[k][j])
DP[i][j] = DP[i][k] + DP[k][j];
}
}
}
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
if (DP[i][j] != INF)
printf("1 ");
else
printf("0 ");
}
printf("\n");
}
return 0;
}
'알고리즘 > 이론' 카테고리의 다른 글
| 유니온 파인드(Union-Find, Disjoint Set) (0) | 2017.06.16 |
|---|---|
| 세그먼트 트리(Segment Tree) (0) | 2017.06.11 |
| 다익스트라(Dijkstra) (0) | 2017.06.11 |
| 이진탐색(Binary Search) (0) | 2017.05.22 |
| 너비 우선 탐색(BFS, Breadth First Search) (0) | 2017.04.22 |




